The point-in-convex-polygon problem : Exploring the 'all sides match' approach

Mar 31, 2025

If you - like me - work in computational-geometry-adjacent spaces (or if you’re a Leetcode hound), you’ve likely come across situations like this:

Does this point lie inside this triangle/rectangle/n-gon ?

Problems like these are really a subset of this more general problem statement:

Given a planar convex n-sided polygon P and a point Q in 3D space, find whether Q lies inside P

There’s a few different ways we could go about this. Here are 3 that I know of:

Checking which side of the edges the point lies.
Using ray-casting / Sunday’s algorithm
Checking whether the point has valid barycentric coordinates

This post explores the first option. Other options will be subjects of future posts1.

Basic assumptions

For the purposes of this post, I’ve assumed the following:

All geometry is 3 dimensional
Any input convex polygon is planar and closed
There are no collinear points on the polygon boundary
All polygon edges have non-zero edge lengths
The boundary points of the polygon will be ordered/given a polygon, an ordered set of boundary points can be found2
I’ll be using double precision for my code (no reason other than increased precision and larger range of numbers)
All point coordinate component values are limited to the maximum and minimum values of the double type. For 64 bit implementations, this is around +/-1.7E³⁰⁸
I will assume that points which are exactly on the boundary of the polygon are also considered to be ‘inside’ the polygon3

Edges, directions and sides

Let’s begin by defining what the heck ‘side’4 means with an example. Consider a polygon and two points - one inside and one outside:

Let’s label the points and assign each segment of the polygon a consistent direction like so:

We could just as easily have chosen to direct these segments opposite to how they’re shown above. For the purposes of this post, it makes no difference.

Having chosen a direction, we then find whether the point is on the left or on the right of each segment (note that we can extend segments as required)

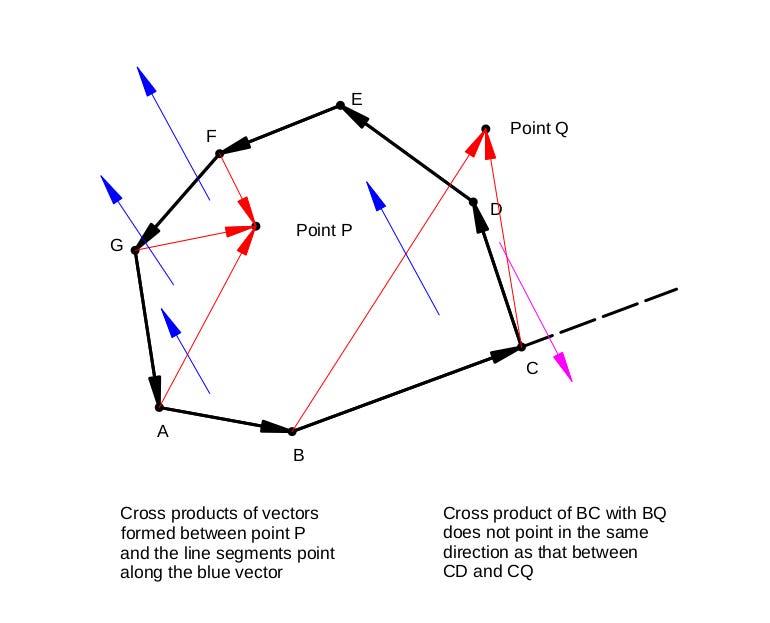
Now here’s the secret sauce: If the point is to the left of all segments (or to the right depending on the direction we chose) then the point must be inside the polygon. But if there is even one segment where the ‘side’ differs, then the point is outside.5

To summarise:

Assume a direction for the polygon segments and loop through them. Find out the ‘side’ on which the point lies for each segment. If the point is on the same ‘side’ for all segments, it is inside the polygon.

This approach works regardless of whether the edge directions of the polygon are clockwise or anti-clockwise.

Note that we don’t explicitly need to know which side the point is relative to the segments, just that the point is on the same side for all segments. This fact will prove useful fairly soon.

Well that seems simple enough. The next question then is - how in the heck do we find which side of a line a point is on ?

Lines, vectors and sides

Say we have a line and a point positioned to its left:

Let’s create outgoing vectors from A to the other two points like so:

And then take the cross product between the vectors AB and AP:

The direction in which the cross product points depends on whether the point is to the right or the left of the line. If P was to the right of AB, the cross product’s direction would be reversed:

So, this cross product approach gives us a sense of the ‘side’ on which a point lies…and that’s all we need really. Recall that to solve our original problem we don’t need to know the ‘side’ for each segment. We just need to check if the point lies on the same ‘side’ for all segments. We can do that by checking if all cross products point along the same direction:

We can check if two vectors are pointing along the same direction (aka are parallel) by taking the dot product of their normalized form. If the dot product is 1.0, then they are indeed parallel6

public bool AreVectorsParallel(Vector3D vecA, Vector3D vecB){
  if(vecA.DotProduct(vecB)/(vecA.Length*vecB.Length) != 1.0){
    return false;
  }
}

Getting down to it

Collecting all of our logic, we can make a simple implementation like so:

public bool IsPointInPolygon(Point3D point, Polygon3D polygon){
  // calculate side of point with first edge  
  Line3D firstSegment = polygon.Segments[0];
  Vector3D pointVec = point - firstSegment.Start;
  Vector3D lineDir = firstSegment.Direction;

  Vector3D firstSide = pointVec.CrossProduct(lineDir);
  double firstSideLength = firstSide.Length;

  for(int i = 1; i< polygon.Count-1; i++){
     pointVec = point - polygon.Segments[i];
     lineDir = polygon.Segments[i+1] - polygon.Segments[i];
     Vector3D side = pointVec.CrossProduct(lineDir);
     double sideLength = side.Length;
     if(side.DotProduct(firstSide)/(sideLength*firstSideLength) != 1.0){
       return false;
     }
  }
  return true;
}

We can make this simpler to test by using an ordered list of points instead of a polygon object:

public bool IsPointInPolygon(Point3D point, IList<Point3D> polygon){
  // calculate side of point with first edge  
  Vector3D lineDir = polygon[1] - polygon[0];
  Vector3D pointVec = point - polygon[0];

  Vector3D firstSide = pointVec.CrossProduct(lineDir);
  double firstSideLength = firstSide.Length;

  for(int i = 1; i< polygon.Count-1; i++){
     pointVec = point - polygon[i];
     lineDir = polygon[i+1] - polygon[i];
     Vector3D side = pointVec.CrossProduct(lineDir);
     double sideLength = side.Length;
     if(side.DotProduct(firstSide)/(sideLength*firstSideLength) != 1.0){
       return false;
     }
  }
  return true;
}

You may have noticed a small bug lurking in that dot product check. Worry not ! We’ll revisit it soon enough.

Not done yet !

In getting here, we forgot to ask a very fundamental question - is the point even on the same plane as the polygon ?7

It seems, then, that in addition to the point-in-polygon problem, we also have to solve this problem:

Given a plane P and a point Q, determine whether Q lies on P

Let’s get into it then.

Points on planes

Say we have an arbitrarily oriented plane in 3D space. We define the plane using local axes X’, Y’ and Z’ relative to the global XYZ system and assume that the plane spans along the X’ and Y’ axes:

Let’s draw a vector between the point Q and the origin of plane P. We can immediately see that if Q is within the plane, the projection of the vector between the point and the plane’s origin on the Z axis of the plane should be a zero vector

Or in code:

public bool IsPointInPlane(Point3D point, Plane3D plane){
  Vector3D vec = point - plane.Origin;
  return vec.DotProduct(plane.z) == 0;
}

Okay. The next question is…

How do we get that plane ?

Let’s have a look at that code we wrote earlier:

public bool IsPointInPlane(Point3D point, Plane3D plane){
  Vector3D vec = point - plane.Origin;
  return vec.DotProduct(plane.z) == 0;
}

Notice that we don’t need the entire Plane3D object. All we really need is the plane’s origin and the z axis vector. Rewriting our earlier code:

public bool IsPointInPlane(Point3D point, Point3D planeOrigin, Vector3D zAxis){
  Vector3D vec = point - planeOrigin;
  return vec.DotProduct(zAxis) == 0;
}

Okay. Now how do we get the origin and z axis vectors ? There’s a few ways to do, so but within the context of our problem, we can use the fact that the polygon is planar and go with the approach below:

Put in code:

public bool IsPointOnPolygonPlane(Point3D point, IList<Point3D> polygon){
  // check if point is in polygon's plane
  Vector3D firstLineDir = polygon[1] - polygon[0];
  Vector3D secondLineDir = polygon[2] - polygon[1];
  Vector3D zVec = firstDir.CrossProduct(secondDir);
  // assuming point[0] as plane origin
  Vector3D pointVec = point - polygon[0];

  if(pointVec.DotProduct(zVec)!=0){
    return false;
  }
}

Note that the planarity check should come before the ‘side’ check since the former is much quicker to assess.

Oh yea, it’s all coming together

Admit it. You read that in Kronk’s voice.

Putting together everything we have gives us this rough sequence of steps:

Choose any 3 consecutive points from the polygon boundary and find its normal vector. Also choose any of these 3 points as plane origin.
Check if point lies in plane. If yes, proceed to 3. Else return false
Create a cycle of vectors using the line segments of the polygon
Loop through each segment and get the ‘side’ of the point using the logic noted above
If the point is on the same ‘side’ for all segments, then return true. If not, return false.

Here’s how it looks in code (Yes it could be cleaner, I was lazy)

public bool IsPointInPolygon(Point3D point, IList<Point3D> polygon){
  /* edge case check. 
  The smallest closed polygon would be a triangle. While normally a triangle would have 3 points, this logic assumes that we add in an extra point at the end of a shape to close out the polygon. So a triangle would have 4 points, with the last point being the same as the first. If the polygon list has 3 points or less, it is not a closed polygon and we return false.
  */
  if(polygon.Count <=3){
    return false; 
  }

  // check if point is in polygon's plane
  Vector3D firstLineDir = polygon[1] - polygon[0];
  Vector3D secondLineDir = polygon[2] - polygon[1];
  Vector3D zVec = firstLineDir.CrossProduct(secondLineDir);
  Vector3D pointVec = point - polygon[0];

  if(pointVec.DotProduct(zVec)!=0){
    return false;
  }

  // calculate side of point with first edge  
  Vector3D firstSide = pointVec.CrossProduct(firstLineDir);
  double firstSideLength = firstSide.Length;

  for(int i = 1; i< polygon.Count-1; i++){
     pointVec = point - polygon[i];
     var lineDir = polygon[i+1] - polygon[i];
     Vector3D side = pointVec.CrossProduct(lineDir);
     double sideLength = side.Length;
     if(side.DotProduct(firstSide)/(sideLength*firstSideLength) != 1.0){
       return false;
     }
  }
  return true;
}

That looks good ! But something’s still missing…

Revisiting the cross product

Have a look at this section of the code:

Vector3D side = pointVec.CrossProduct(lineDir);

Here’s a question : what would happen if the value of the cross product was a zero vector ?

Yep, we forgot to account for this. A zero vector resultant from a cross product operation here means one of 3 cases:

the point vector itself is a zero vector (since polygon edges with zero lengths aren’t allowed per our initial assumptions), or
the point vector is parallel to the edge vector
the point vector is anti-parallel to the edge vector

Zero point vector

To verify this, we just check the length of the vector AP. If it’s zero, we return true (since the point is coincident with a boundary point and is, therefore, inside the polygon). If not, then we go to the parallel/anti-parallel check

Parallel or anti-parallel

We can check this via the dot product. If the dot product is positive, the vectors are parallel. If negative, they’re anti-parallel. This stems from the fact that the dot product of any two vectors includes a cosine of the angle between them, and cos(0^o) is positive while cos(180^o) is negative.8

If parallel

In this case, the point lies somewhere in the same direction as the edge vector, and we must consider two situations:

The point either lies on the edge, or
The point lies away from the edge

These situations are noted in the image below:

If anti-parallel

In this case, given our initial assumptions the point will invariably be outside the polygon9

We can account for all 3 cases like so:

boolean check = pointVec.Length == 0 ||
                  (pointVec.DotProduct(firstLineDir) > 0 &&
                   pointVec.Length < firstLineDir.Length);

And here’s the updated code to go with it:

public bool IsPointInPolygon(Point3D point, IList<Point3D> polygon){
  /* edge case check. 
  The smallest closed polygon would be a triangle. While normally a triangle would have 3 points, this logic assumes that we add in an extra point at the end of a shape to close out the polygon. So a triangle would have 4 points, with the last point being the same as the first. If the polygon list has 3 points or less, it is not a closed polygon and we return false.
  */
  if(polygon.Count <=3){
    return false; 
  }

  // check if point is in polygon's plane
  Vector3D firstLineDir = polygon[1] - polygon[0];
  Vector3D secondLineDir = polygon[2] - polygon[1];
  Vector3D zVec = firstLineDir.CrossProduct(secondLineDir);
  Vector3D pointVec = point - polygon[0];

  if(pointVec.DotProduct(zVec)!=0){
    return false;
  }

  // calculate side of point with first edge  
  Vector3D firstSide = pointVec.CrossProduct(firstLineDir);
  double firstSideLength = firstSide.Length;
  if (firstSideLength == 0){
    return pointVec.Length == 0 ||
          (pointVec.DotProduct(firstLineDir) > 0 &&
           pointVec.Length < firstLineDir.Length);
  }

  for(int i = 1; i< polygon.Count-1; i++){
     pointVec = point - polygon[i];
     var lineDir = polygon[i+1] - polygon[i];
     Vector3D side = pointVec.CrossProduct(lineDir);
     double sideLength = side.Length;
     if (sideLength == 0){
       return pointVec.Length == 0 ||
          (pointVec.DotProduct(lineDir) > 0 &&
           pointVec.Length < lineDir.Length);
     }
     if(side.DotProduct(firstSide)/(sideLength*firstSideLength) != 1.0){
       return false;
     }
  }
  return true;
}

With that, we’re good to go ahead and test.

Testing

Here are three simple tests using a triangle as the input polygon:

[Test]
public void Test_PointOutsidePolygon_ShouldReturnFalse()
{
    var point = new Point3D(0, 0, 0);
    IList<Point3D> polygon = new List<Point3D>();
    
    polygon.Add(new Point3D(10, 10, 10));
    polygon.Add(new Point3D(15, 10, 10));
    polygon.Add(new Point3D(10, 15, 10));
    polygon.Add(new Point3D(10, 10, 10));

    Assert.False(Utility.IsPointInPolygon(point, polygon));
}

[Test]
public void Test_PointInsidePolygon_ShouldReturnTrue()
{
    var point = new Point3D(11, 11, 10);
    IList<Point3D> polygon = new List<Point3D>();
    
    polygon.Add(new Point3D(10, 10, 10));
    polygon.Add(new Point3D(15, 10, 10));
    polygon.Add(new Point3D(10, 15, 10));
    polygon.Add(new Point3D(10, 10, 10));

    Assert.True(Utility.IsPointInPolygon(point, polygon));
}

[Test]
public void Test_PointOnPolygon_ShouldReturnTrue()
{
    var point = new Point3D(10.5, 10.0, 10);
    IList<Point3D> polygon = new List<Point3D>();
    
    polygon.Add(new Point3D(10, 10, 10));
    polygon.Add(new Point3D(15, 10, 10));
    polygon.Add(new Point3D(10, 15, 10));
    polygon.Add(new Point3D(10, 10, 10));

    Assert.True(Utility.IsPointInPolygon(point, polygon));
}

These simple tests all pass. But let’s try something a bit more complex. The test below also uses a triangle and a point that lies on one of the edges, but the coordinates are no longer integers:

[Test]
public void Test_PointOnPolygon_2_ShouldReturnTrue()
{
    double x1 = 1.0/10;
    double y1 = 1.0/9;
    double x2 = 100.0/8;
    double y2 = 100.0/3;
    double x3 = 100.0/4;
    double y3 = 100.0/9;

    double point_x = x1 + (3.0 / 7) * (x2 - x1);
    double point_y = y1 + (3.0 / 7) * (y2 - y1);
    IList<Point3D> polygon = new List<Point3D>();
    
    polygon.Add(new Point3D(x1, y1, 10));
    polygon.Add(new Point3D(x2, y2, 10));
    polygon.Add(new Point3D(x3, y3, 10));
    polygon.Add(new Point3D(x1, y1, 10));
    
    var point = new Point3D(point_x, point_y, 10);

    Assert.True(Utility.IsPointInPolygon(point, polygon));
}

Here, the input point is on the segment (x1, y1) to (x2, y2). We would expect our logic to return true, and yet….

Let’s jump into debug mode to see what’s going on:

Aha ! In theory, the point is bang on the line segment so the cross product should return zero. And yet, firstSideLength is not zero but a very small value instead.

Remember that small bug I hinted at in the earlier sections ? Well this is it. We’ve just been hit by a floating point error.

To put a very large topic into a very small amount of text : floating point numbers are not able to represent all possible numbers on the number line accurately and errors can and do pop up. In most cases these errors are small, but sometimes these errors can cause unexpected side effects (like the one we just saw).10

One quick and easy way to fix this is to account for the error by way of tolerances.

Tolerance/Precision

Everything in computational geometry works within some level of tolerance. If we don’t specify anything, most programs will just use the default tolerance of the numeric types used to represent the point and vector components (e.g. if we represent a point with a double, in most programming languages that means we work with a tolerance/precision of about 10^-16 (source). For most cases you’d think that’s plenty … but there are edge cases where even seemingly normal inputs can result in exceptionally weird results, all due to tolerances.

I could go on, but a topic like tolerances in geometry deserves its own blog post. For now, to fix the error we can add a generic tolerance like so:

public bool IsPointInPolygon(Point3D point, IList<Point3D> polygon, double tolerance){
  /* edge case check. 
  The smallest closed polygon would be a triangle. While normally a triangle would have 3 points, this logic assumes that we add in an extra point at the end of a shape to close out the polygon. So a triangle would have 4 points, with the last point being the same as the first. If the polygon list has 3 points or less, it is not a closed polygon and we return false.
  */
  if(polygon.Count <=3){
    return false; 
  }

  // check if point is in polygon's plane
  Vector3D firstLineDir = polygon[1] - polygon[0];
  Vector3D secondLineDir = polygon[2] - polygon[1];
  Vector3D zVec = firstLineDir.CrossProduct(secondLineDir);
  Vector3D pointVec = point - polygon[0];

  if(Math.Abs(pointVec.DotProduct(zVec)) > tolerance){
    return false;
  }

  // calculate side of point with first edge  
  Vector3D firstSide = pointVec.CrossProduct(firstLineDir);
  double firstSideLength = firstSide.Length;
  if (firstSideLength <= tolerance){
    return pointVec.Length <= tolerance ||
          (pointVec.DotProduct(firstLineDir) > 0 &&
           pointVec.Length < firstLineDir.Length);
  }

  for(int i = 1; i< polygon.Count-1; i++){
     pointVec = point - polygon[i];
     var lineDir = polygon[i+1] - polygon[i];
     Vector3D side = pointVec.CrossProduct(lineDir);
     double sideLength = side.Length;
     if (sideLength <= tolerance){
       return pointVec.Length <= tolerance ||
          (pointVec.DotProduct(lineDir) > 0 &&
           pointVec.Length < lineDir.Length);
     }
     if(Math.Abs(1-side.DotProduct(firstSide)/(sideLength*firstSideLength)) > tolerance){
        return false;
     }
  }
  return true;
}

Choosing a tolerance value depends on a multitude of factors, but in my (admittedly limited) experience, using something around 1E^-10 seems to work well for most cases11.

Indeed, with 1E^-10, all of our test cases now pass:

And that’s it …. is what you thought I’d say ! One of the last things we can (and given that it’s computational geometry - should) look at is speed.

How fast is it ?

Quite ! Here’s two benchmarks (run using BenchmarkDotNet with default settings) on my test rig for a point that lies inside a triangle and a hexagon:

As expected, barring any short-circuiting exits (e.g. point not in plane), solve time scales linearly with the number of sides (since each side adds an additional loop iteration). Our approach is O(n), with n being the number of sides in the input polygon.

Can we make it faster ?

Yes we can. Here’s a few practical things we can do:

Bounding box as pre-validation

The idea is to compare the point coordinates against the bounding box of the polygon12 before we run the point-in-plane or the ‘side check’ logic. If the point’s coordinates are outside the range of the bounding box, we can quickly return false

Note - this is only useful if we have a large number of points with a good spread. If, instead, we have lots of points clustered close to the polygon in question, this logic can actually slow down our calculations a tiny bit due to the extra CPU cycles spent validating points against the bounding box.

SIMD

Using SIMD can offer a fair bump-up in speed, the tradeoff being the code can (more likely will) be harder to read and maintain. I’ll make a separate post about how we can refactor our code with SIMD later but if anyone’s interested in knowing more, MS has a really good post about SIMD intrinsics in C# here: https://devblogs.microsoft.com/dotnet/hardware-intrinsics-in-net-core/

A different algorithm ?

There is a well-studied approach that reduces the problem from O(n) to O(logn). I will explore this in more detail in a future post, but if anyone’s curious, this page has a nice writeup about it: https://cp-algorithms.com/geometry/point-in-convex-polygon.html

Code and stuff

All code shown in this blog (along with benchmark and other test code) can be found on my github repo here: https://github.com/andorrax101/PointInPolygon

Miscellaneous

No LLMs were used in making this post. All non-meme images have been made using QCAD. All meme images were taken from imgur.

The topic of this post is itself a subset of a more general point-in-polygon problem where the polygons could be concave or convex. I’ll write about this general case in a seprate blog post in future.

The order of points or segments gives us the ‘winding sense’ of the polygon. For closed planar polygons, the winding sense is either clockwise or anti-clockwise.

Technically, they should be considered as ‘on’ the polygon. However for the purposes of this post I’m inferring ‘inside’ to simply mean ‘not outside’, and points on the polygon boundary are definitely not outside the polygon.

It’s worth noting that this approach is also referred to as one where the point lies within the same halfspace for all edges. For a general overview on halfspaces, I recommend going through the Real Time Collision Detection book referenced in the further reading section.

This can only work with convex polygons (where each internal angle is less than 180 degrees)

This follows from the fact that the angle between two parallel vectors is zero, and dot product of two unit vectors is the cosine of the angle between them, and cos(0) is 1.0

We would not need to do this check if we were working in 2D, but we chose to work in 3D…doh !

I’ve specifically used positive and negative here instead of 1.0 and -1.0 because floating point errors can sometimes cause dot products to not exactly equal 1.0 or -1.0.

Since we’ve assumed that our polygon is convex and does not have collinear boundary points, this is the only remaining option

I thoroughly recommend going through the paper What every computer scientist should know about floating point arithmetic : https://www.itu.dk/~sestoft/bachelor/IEEE754_article.pdf

This tolerance value is specifically for double types. If using floats, a different tolerance should be used.

Credits for this idea go to the author of this blog post :https://totologic.blogspot.com/2014/01/accurate-point-in-triangle-test.html

Andorrax101’s Substack

Discussion about this post